Statistical Inference: Hypothesis Testing Theory
- sujonodamario

- Apr 19, 2021
- 2 min read
Hypothesis Testing is a decision-making procedure in statistics with the goal to whether accept or reject a statement of some parameter. Hypotheses are statements about the population and we want to determine whether the values we acquire from the samples are statistically justified.
This method compares two hypotheses: null hypothesis (H0) and alternative hypothesis (H1). For example, we want to know whether a mean of one population equals 30, hence, the null hypothesis is μ = 30 and the alternative one is μ ≠ 30.
The specified value in the hypothesis (30 in the previous example) could be obtained from three possible ways and it influences the objective of conducting the hypothesis testing itself. First, the number is a result from past knowledge or experience of one process, then the hypothesis testing aims to determine the change of a parameter.
Second, the value is formulated from a theory or mathematical model, hence proving such theory is the focus of the hypothesis testing. Lastly, the value is acquired from specific procedure or specifications, then the hypothesis testing is conformance testing, a test of whether one process follows the given procedure or rules.
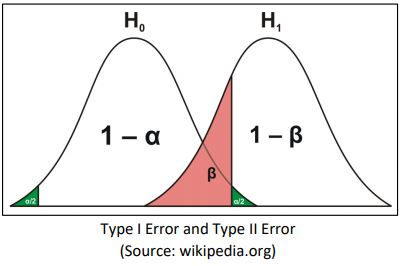
In Hypothesis testing, two wrong conclusions could emerge. The first one is called type I Error and it occurs when rejecting the null hypothesis when it is true. On the other hand, failing to reject (accepting) the null hypothesis when it is actually false is defined as a type II Error.
Since the data samples are basically random variables, we could determine the probabilities of getting type I Error or type II Error, namely α and β respectively. These two errors are related to each other, meaning a decrease in the probability of one error type always increases the probability of the other error type. Moreover, this information could provide an insight into the power of statistical test: the probability of correctly rejecting a false null hypothesis.




Comments